Week 12 · Similarity and Clustering
John Ashley Burgoyne
20 March 2019
compmus-w12.RmdSet-up
All of the tools that are strictly necessary for clustering are
available in base R. For full flexibility, however, the
protoclust packages is recommended. If you want to explore
further possibilities, look at the cluster package.
## ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.2 ──
## ✔ ggplot2 3.4.1 ✔ purrr 1.0.1
## ✔ tibble 3.1.8 ✔ dplyr 1.1.0
## ✔ tidyr 1.3.0 ✔ stringr 1.5.0
## ✔ readr 2.1.4 ✔ forcats 1.0.0
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag() masks stats::lag()## ── Attaching packages ────────────────────────────────────── tidymodels 1.0.0 ──
## ✔ broom 1.0.3 ✔ rsample 1.1.1
## ✔ dials 1.1.0 ✔ tune 1.0.1
## ✔ infer 1.0.4 ✔ workflows 1.1.2
## ✔ modeldata 1.1.0 ✔ workflowsets 1.0.0
## ✔ parsnip 1.0.3 ✔ yardstick 1.1.0
## ✔ recipes 1.0.4
## ── Conflicts ───────────────────────────────────────── tidymodels_conflicts() ──
## ✖ scales::discard() masks purrr::discard()
## ✖ dplyr::filter() masks stats::filter()
## ✖ recipes::fixed() masks stringr::fixed()
## ✖ dplyr::lag() masks stats::lag()
## ✖ yardstick::spec() masks readr::spec()
## ✖ recipes::step() masks stats::step()
## • Learn how to get started at https://www.tidymodels.org/start/##
## Attaching package: 'spotifyr'
##
## The following object is masked from 'package:yardstick':
##
## tidy
##
## The following object is masked from 'package:rsample':
##
## tidy
##
## The following object is masked from 'package:recipes':
##
## tidy
##
## The following object is masked from 'package:parsnip':
##
## tidy
##
## The following object is masked from 'package:broom':
##
## tidy
library(compmus)In order for the code below to run, it is also necessary to set up
Spotify login credentials for spotifyr.
Clustering
The Bibliothèque nationale de France (BnF) makes a large portion of its music collection available on Spotify, including an eclectic collection of curated playlists. The defining musical characteristics of these playlists are sometimes unclear: for example, they have a Halloween playlist. Perhaps clustering can help us organise and describe what kinds of musical selections make it into the BnF’s playlist.
We begin by loading the playlist and summarising the pitch and timbre
features, just like last week. Note that, also like last week, we use
compmus_c_transpose to transpose the chroma features so
that – depending on the accuracy of Spotify’s key estimation – we can
interpret them as if every piece were in C major or C minor. Although
this example includes no delta features, try adding them yourself if you
are feeling comfortable with R!
halloween <-
get_playlist_audio_features('bnfcollection', '1vsoLSK3ArkpaIHmUaF02C') %>%
add_audio_analysis %>%
mutate(
segments =
map2(segments, key, compmus_c_transpose)) %>%
mutate(
pitches =
map(segments,
compmus_summarise, pitches,
method = 'mean', norm = 'manhattan'),
timbre =
map(
segments,
compmus_summarise, timbre,
method = 'mean')) %>%
mutate(pitches = map(pitches, compmus_normalise, 'clr')) %>%
mutate_at(vars(pitches, timbre), map, bind_rows) %>%
unnest(cols = c(pitches, timbre))Pre-processing
Remember that in the tidyverse approach, we can
preprocess data with a recipe. In this case, instead of a
label that we want to predict, we start with a label that will make the
cluster plots readable. For most projects, the track name will be the
best choice (although feel free to experiment with others). The code
below uses str_trunc to clip the track name to a maximum of
20 characters, again in order to improve readability. The other change
from last week is column_to_rownames, which is necessary
for the plot labels to appear correctly.
Last week we also discussed that although standardising variables
with step_center to make the mean 0 and
step_scale to make the standard deviation 1 is the most
common approach, sometimes step_range is a better
alternative, which squashes or stretches every features so that it
ranges from 0 to 1. For most classification algorithms, the difference
is small; for clustering, the differences can be more noticable. It’s
wise to try both.
halloween_juice <-
recipe(track.name ~
danceability +
energy +
loudness +
speechiness +
acousticness +
instrumentalness +
liveness +
valence +
tempo +
track.duration_ms +
C + `C#|Db` + D + `D#|Eb` +
E + `F` + `F#|Gb` + G +
`G#|Ab` + A + `A#|Bb` + B +
c01 + c02 + c03 + c04 + c05 + c06 +
c07 + c08 + c09 + c10 + c11 + c12,
data = halloween) %>%
step_center(all_predictors()) %>%
step_scale(all_predictors()) %>%
# step_range(all_predictors()) %>%
prep(halloween %>% mutate(track_name = str_trunc(track.name, 20))) %>%
juice %>%
column_to_rownames('track.name')Computing distances
When using step_center and step_scale, then
the Euclidean distance is usual. When using step_range,
then the Manhattan distance is also a good choice: this combination is
known as Gower’s distance and has a long history in
clustering.
halloween_dist <- dist(halloween_juice, method = 'euclidean')Hierarchical clustering
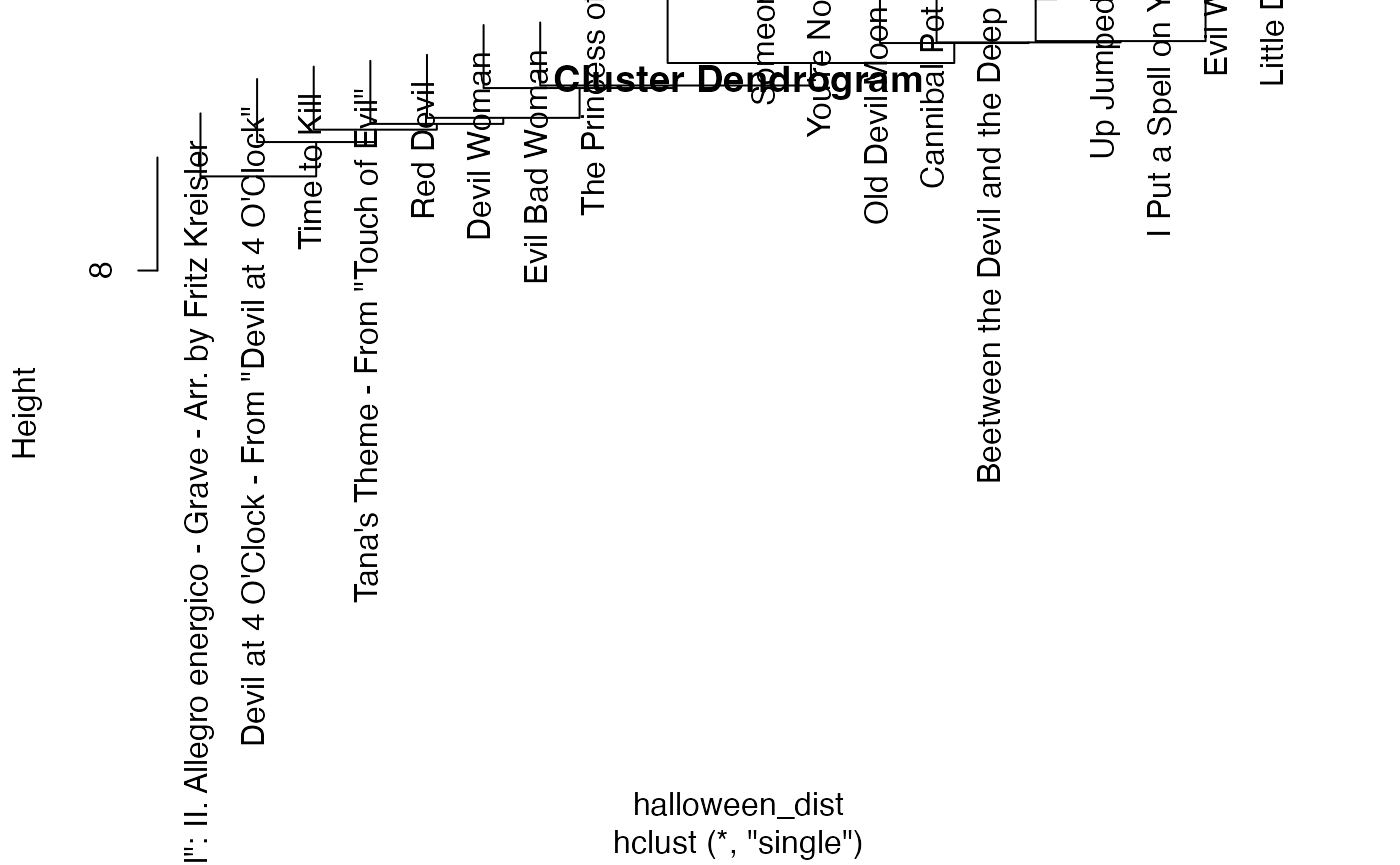
As you learned in your DataCamp exercises this week, there are three
primary types of linkage: single, average, and complete.
Usually average or complete give the best results. We can use the
ggendrogram function to make a more standardised plot of
the results.
A more recent – and often superior – linkage function is minimax
linkage, available in the protoclust package. It is
more akin to \(k\)-means: at each step,
it chooses an ideal centroid for every cluster such that the maximum
distance between centroids and all members of their respective clusters
is as small as possible.
protoclust(halloween_dist) %>% plot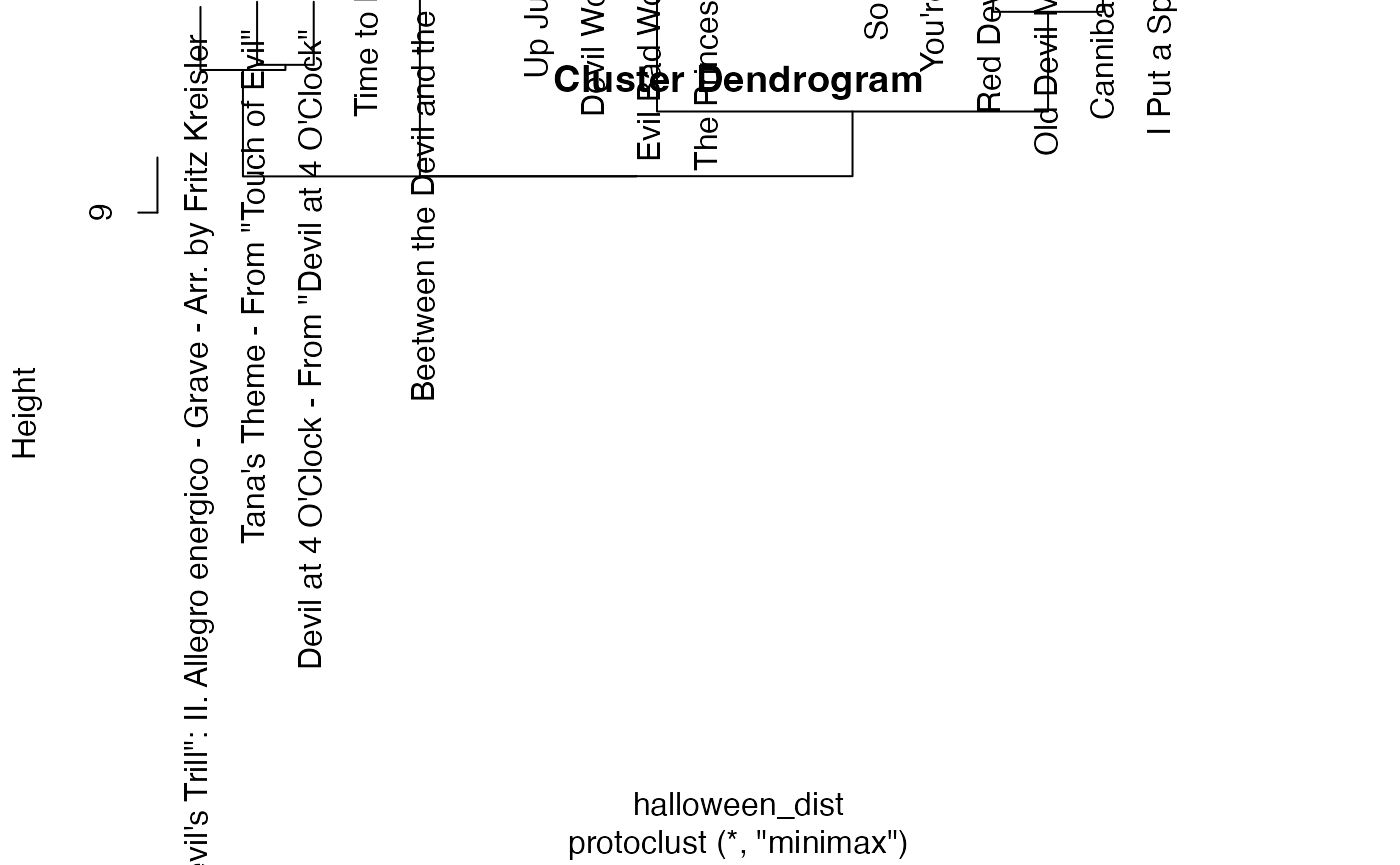
Try all four of these linkages. Which one looks the best? Which one sounds the best (when you listen to the tracks on Spotify)? Can you guess which features are separating the clusters?
k-Means
Unlike hierarchical clustering, k-means clustering returns a different results every time. Nonetheless, it can be a useful reality check on the stability of the clusters from hierarchical clustering.
kmeans(halloween_juice, 4)## K-means clustering with 4 clusters of sizes 2, 6, 7, 5
##
## Cluster means:
## danceability energy loudness speechiness acousticness instrumentalness
## 1 0.09605479 0.07213439 0.5262965 -0.48145689 0.1384264 1.105519968
## 2 0.83101946 1.15415030 0.6751792 0.92760310 -0.5974045 -0.059112255
## 3 -1.20286793 -0.65481004 -0.8180242 -0.69484670 0.1960202 -0.002641033
## 4 0.64836983 -0.49710006 0.1245002 0.05224442 0.3870865 -0.367575835
## liveness valence tempo track.duration_ms C C#|Db
## 1 0.23473711 0.1471131 -0.02038562 -0.12645737 0.44130883 -1.77309313
## 2 -0.69972953 0.9450583 0.65014905 -0.32295764 0.10302548 0.02907237
## 3 0.08514692 -1.0319293 -0.13884228 0.36331312 0.03424285 0.12208631
## 4 0.62657491 0.2517858 -0.57764542 -0.07050626 -0.34809410 0.50342957
## D D#|Eb E F F#|Gb G
## 1 1.3525471 -0.5766835 1.7594651 -0.5345336 -0.4481507 0.17806751
## 2 0.1496190 -0.1653766 -0.1800450 0.3505671 0.4983636 -0.34465054
## 3 -0.2036450 0.6233577 0.4252545 0.3213209 -0.6423839 -0.09781781
## 4 -0.4354586 -0.4435755 -1.0830882 -0.6567164 0.4805615 0.47929858
## G#|Ab A A#|Bb B c01 c02
## 1 -2.0105648218 1.2442431 -1.91137400 1.8355507 0.9626355 1.2067481
## 2 -0.1988474363 -0.2919318 -0.06307911 0.2556722 0.5016825 0.3531571
## 3 0.0001152723 -0.3356205 0.03918216 -0.3162802 -0.2106414 -0.2500977
## 4 1.0426814710 0.3224897 0.78538950 -0.5982347 -0.6921753 -0.5563510
## c03 c04 c05 c06 c07 c08
## 1 1.7439574 1.40708521 0.5926782 0.1993832 -0.998983423 -1.4265712
## 2 -0.5880053 0.53833638 -0.5492119 0.2363025 0.472074517 -0.0128682
## 3 0.3978360 -0.81726256 0.1383504 -0.8499680 -0.001680086 0.1770037
## 4 -0.5489469 -0.06467015 0.2282925 0.8266389 -0.164543931 0.3382651
## c09 c10 c11 c12
## 1 -0.9808208 -0.4151848 0.5479418 -0.2223407
## 2 -0.8325366 0.5484503 -0.4237820 -0.3920377
## 3 0.4068887 -0.6793797 0.9025014 0.6023293
## 4 0.8217280 0.4590651 -0.9741404 -0.2838794
##
## Clustering vector:
## I Put a Spell on You
## 2
## Close Your Eyes
## 3
## Evil Woman
## 2
## Time to Kill
## 4
## Evil Bad Woman
## 4
## The Princess of Evil
## 3
## 'Round Midnight
## 3
## Tana's Theme - From "Touch of Evil"
## 1
## Evil Blues
## 4
## Someone Is Watching
## 3
## Violin Sonata in G Minor "Devil's Trill": II. Allegro energico - Grave - Arr. by Fritz Kreisler
## 1
## Cannibal Pot
## 2
## Red Devil
## 2
## You're Not Living in Vain
## 3
## Little Demon
## 2
## Devil at 4 O'Clock - From "Devil at 4 O'Clock"
## 3
## Old Devil Moon
## 2
## Up Jumped the Devil
## 4
## Beetween the Devil and the Deep Blue Sea
## 4
## Devil Woman
## 3
##
## Within cluster sum of squares by cluster:
## [1] 29.47158 127.08694 139.55752 104.86406
## (between_SS / total_SS = 37.9 %)
##
## Available components:
##
## [1] "cluster" "centers" "totss" "withinss" "tot.withinss"
## [6] "betweenss" "size" "iter" "ifault"